CBSE Class 11th Work done by a variable force Details & Preparations Downloads
In the intricate dance of forces and motions that govern the physical world, the concept of work done plays a central role. While the understanding of work done by a constant force is well-established, the narrative becomes more nuanced when we venture into the realm of variable forces. In this exploration, we will unravel the intricacies of work done by a force that changes along the path of motion.

Defining the Work Done:
Work done (W) is a fundamental concept in physics, representing the energy transferred to or from an object as a result of a force acting on it, causing it to move a certain distance. When the force acting on an object remains constant, as is often assumed in introductory physics, calculating work is a straightforward multiplication of force and displacement (W=F⋅d). However, real-world scenarios frequently involve forces that vary along the path of motion, requiring a deeper dive into the dynamics of the system.
Mathematical Expression of Variable Work
For a variable force
F(x) acting over an infinitesimally small displacement dx, the infinitesimal work done (dW) is expressed as the product of force and displacement:
dW=F(x)⋅dx
To find the total work done, the process involves integrating this expression over the entire displacement:
W=∫F(x)dx
This integration, a cornerstone of calculus, allows us to sum up the work done at each infinitesimally small segment along the path, taking into account the changing force.

Graphical Insight: Tracing the Force-Displacement Curve
Visualising the work done by a variable force often involves examining the force-displacement graph. The area under this curve represents the total work done. Regions where the force is positive contribute positively to the work, while regions with negative force values contribute negatively. This graphical representation offers an intuitive understanding of how the force varies and the impact on the overall work done.
Real-world Applications: A Glimpse into Dynamics
Understanding work done by variable forces is not just an abstract concept but a key player in various real-world scenarios. Consider a scenario where an object is pulled or pushed with a force that changes at different points in its journey. Examples include:
1. Spring Systems:
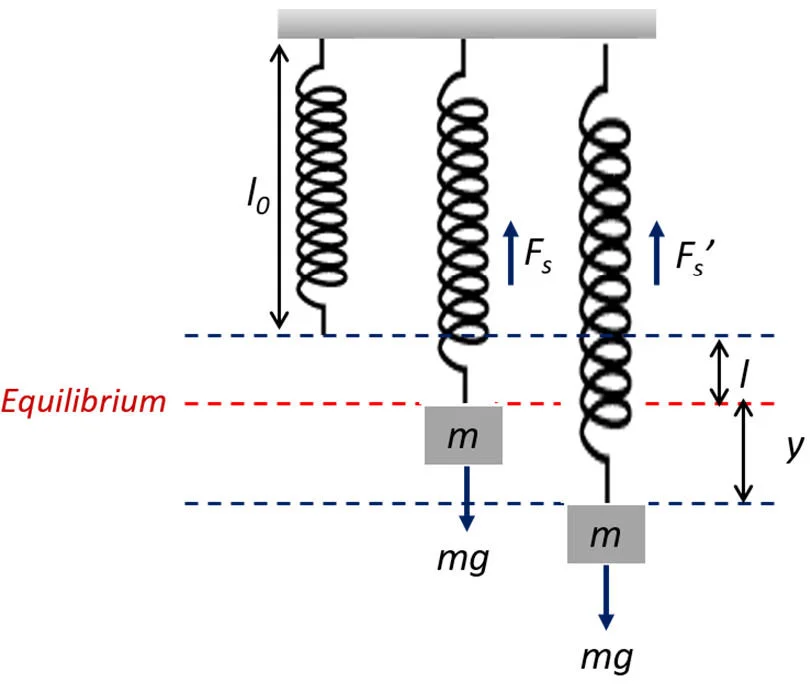
-
Work done in stretching or compressing a spring involves a variable force, dictated by Hooke's Law ( F=−kx), where k is the spring constant and x is the displacement from equilibrium. Integrating this force over displacement reveals the total work done on the spring.
2. Frictional Forces:

-
Work done against friction, a force that often varies depending on factors like the nature of surfaces in contact, showcases the dynamic nature of forces in motion.
Conservative and Non-conservative Forces: A Dichotomy
Variable forces can be categorised into conservative and non-conservative forces. Conservative forces, such as gravity, allow for a potential energy function. In such cases, the work done is path-independent, and the total work done is the change in potential energy. On the other hand, non-conservative forces, like friction, may lead to energy dissipation and require a more intricate analysis.
Insights from the Work-Energy Theorem
The work-energy theorem is a guiding principle in understanding the interplay between work and kinetic energy. For a variable force, the theorem states that the net work done ( W net) is equal to the change in kinetic energy (ΔKE) of the object:
W net=ΔKE
This succinctly captures the essence of how the work done by variable forces influences the motion and energy state of an object.
Challenges and Complexities: Realising the Dynamic Nature
While the mathematical expressions and graphical insights provide a structured framework, the analysis of work done by variable forces introduces challenges. Integrating complex force functions and navigating through intricate force-displacement curves require a solid grasp of mathematical tools and a keen eye for graphical interpretation.
CBSE Class 11th Downloadable Resources:
| 1. CBSE Class 11th Topic Wise Summary | View Page / Download |
| 2. CBSE Class 11th NCERT Books | View Page / Download |
| 3. CBSE Class 11th NCERT Solutions | View Page / Download |
| 4. CBSE Class 11th Exemplar | View Page / Download |
| 5. CBSE Class 11th Previous Year Papers | View Page / Download |
| 6. CBSE Class 11th Sample Papers | View Page / Download |
| 7. CBSE Class 11th Question Bank | View Page / Download |
| 8. CBSE Class 11th Topic Wise Revision Notes | View Page / Download |
| 9. CBSE Class 11th Last Minutes Preparation Resources | View Page / Download |
| 10. CBSE Class 11th Best Reference Books | View Page / Download |
| 11. CBSE Class 11th Formula Booklet | View Page / Download |
Being in CBSE class 11th and considering the board examinations you must be needing resources to excel in your examinations. At TestprepKart we take great pride in providing CBSE class 11th all study resources in downloadable form for you to keep you going.
Below is the list of all CBSE class 11th Downloads available on TestprepKart for both Indian and NRI students preparing for CBSE class 11th in UAE, Oman, Qatar, Kuwait & Bahrain.
SAMPLE PRACTICE QUESTIONS OF SIGNIFICANT FIGURES:
Q1 What is work done by a force?
Answer 1 Work done by a force is the product of the force applied to an object and the displacement of the object in the direction of the force. Mathematically, it is given by the formula W=∫Fdx, where W is work, F is the force, and dx is the displacement.
Q2 How is work done by a variable force different from constant force?
Answer 2 When the force acting on an object is constant, the calculation is straightforward (W=F⋅d). In the case of a variable force, the force may change at different points along the displacement, requiring integration to find the total work done.
Q3 What is the significance of a variable force in physics?
Answer 3 Variable forces are common in real-world scenarios. Understanding work done by variable forces is crucial for analyzing systems where forces change over time or position, such as springs, gravitational fields, or electromagnetic forces.
Q4 How is work done by a variable force calculated graphically?
Answer 4 The work done by a variable force can be calculated graphically by finding the area under the force-displacement curve. The integral of the force-displacement function over the given range provides the total work done.
Q5 What is the unit of work?
Answer 5 The unit of work is the joule (J). One joule is equal to one newton-meter (N·m), which represents the amount of work done when a force of one newton displaces an object by one meter in the direction of the force.

| Class 11th CBSE Physics Chapters |
| Chapter1: UNITS AND MEASUREMENTS |
| Chapter2: MOTION IN A STRAIGHT LINE |
| Chapter3: MOTION IN A PLANE |
| Chapter4: LAWS OF MOTION |
| Chapter5: WORK, ENERGY AND POWER |
| > Introduction |
| > Notions of work and kinetic energy: The work-energy theorem |
| > Work |
| > Kinetic energy |
| > The concept of potential energy |
| > The conservation of mechanical energy |
| > The potential energy of a spring |
| > Power |
| > Collisions |
| Chapter6: SYSTEM OF PARTICLES AND ROTATIONAL MOTION |
| Chapter7: GRAVITATION |
| Chapter8: MECHANICAL PROPERTIES OF SOLIDS |
| Chapter9: MECHANICAL PROPERTIES OF FLUIDS |
| Chapter10: THERMAL PROPERTIES OF MATTER |
| Chapter12: KINETIC THEORY |
| Chapter13: OSCILLATIONS |
| Chapter14: WAVES |
| Class 11th CBSE Chemistry Chapters |
| Chapter1: SOME BASIC CONCEPTS OF CHEMISTRY |
| Chapter2: STRUCTURE OF ATOMS |
| Chapter3: CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES |
| Chapter4: CHEMICAL BONDING AND MOLECULAR STRUCTURE |
| Chapter5: THERMODYNAMICS |
| Chapter6: EQUILIBRIUM |
| Chapter7: REDOX REACTIONS |
| Chapter8: ORGANIC CHEMISTRY - SOME BASIC PRINCIPLE AND TECHNIQUES |
| Chapter9: Hydrocarbons HYDROCARBONS |
| Class 11th CBSE Mathematics chapter |
| Chapter1: SETS |
| Chapter2: RELATIONS AND FUNCTIONS |
| Chapter3: TRIGONOMETRIC FUNCTIONS |
| Chapter4: COMPLEX NUMBER AND QUADRATIC EQUATIONS |
| Chapter5: LINEAR INEQUALITIES |
| Chapter6: PERMUTATIONS AND COMBINATIONS |
| Chapter7: BINOMIAL THEOREM |
| Chapter8: SEQUENCES AND SERIES |
| Chapter9: STRAIGHT LINES |
| Chapter10: CONIC SECTIONS |
| Chapter11: INTRODUCTION TO THREE-DIMENSIONAL GEOMETRY |
| Chapter12: LIMITS AND DERIVATIVES |
| Chapter13: STATISTICS |
| Chapter14: PROBABILITY |
| Class 8 Link soon |
| Class 9 Link soon |
| Class 10 Link soon |
| Class 12 Link soon |