The Complete IB Math Syllabus SL / HL 2021 (updated)
Mathematical Studies Standard Level Mathematics Standard Level Mathematics Higher level Further Mathematics Higher Level (Final exam- May 2020) Download Complete IB Maths Syllabus Old Mathematics SL Students who are interested in mathematics Are fairly moderate at it Keen to study courses involving mathematics after high school (Eg. Economics & Sciences) Number and Algebra (19 Hours) Functions (21 Hours) Geometry and Trigonometry (25 Hours) Probability and Statistics (27 Hours) Calculus (28 Hours) Toolkit and Exploration (30 hours) Addition of Syllabus Deduction of Syllabus Simple deductive proof Vectors z on y regression line Volume of revolution Regression Old Mathematics HL Students who love Mathematics Are very strong at it Interested in studying courses that highly involve math after high school (Eg. Engineering) Get Free IB Trial Session Download IB Math eBook Number and Algebra (39 Hours) Functions (32 Hours) Geometry and Trigonometry (51 Hours) Probability and Statistics (33 Hours) Calculus (55 Hours) Toolkit and Exploration (30 hours) Addition Of Syllabus Deduction Of syllabus Binomial Theorem Poisson Distribution Partial Fractions Graphs (more depth) Sampling and Statistics Correlation and regression L’Hospital’s rule and Applications Differential Equations Maclaurin Series Old Math Studies Students who are not strong at math Do not plan to study any mathematics-based course after high school Number and Algebra (16 Hours) Functions (31 Hours) Geometry and Trigonometry (18 Hours) Probability and Statistics (36 Hours) Calculus (19 Hours) Toolkit and Exploration (30 hours) Addition of Syllabus Deduction of Syllabus Sigma notation Number sets Amortization and Annuities Currency conversion System of Equations Logic (All 20 hours) General probability distributions Most of Set theory Binomial Distribution Correlation coefficient Chi squared Equation of perpendicular bisectors Voronoi diagrams and Applications Function modelling Basic Integration Unlike old courses Number and Algebra (29 Hours) Functions (42 Hours) Geometry and Trigonometry (46 Hours) Probability and Statistics (52 Hours) Calculus (41 Hours) Toolkit and Exploration (30 hours) Addition HL Content Log and Exponent laws Sum of infinite geometric sequences Complex Numbers Matrices. Eigenvalues and Eigenvectors Composite Functions, Inverse, Transformations Function modelling Radians, Trig identities, Trig equations Geometry transformations using matrices Vectors Graph Theory Non-linear regression More sophistication with random variables and distribution (Poisson) Steady state and long term probabilities (transition matrices, Markov Chains) Derivatives, Second derivatives Integration, Area, Volume Kinematics Differential Equations Slope fields Sampling and data collection methods Mathematics: Applications and Interpretation Mathematics: Analysis and Approaches UNIVERSITY COURSE SL HL SL HL University Of Oxford Requiring Math ✖ ✔ ✖ ✔ Other courses ✔ ✔ ✔ ✔ University Of Cambridge Requiring Math ✖ ✖ ✖ ✔ Other courses ✔ ✔ ✔ ✔ University Of Edinburgh Requiring Math ✖ ✖ ✔ ✔ Other courses ✔ ✔ ✔ ✔ University Of Bristol Requiring Math HL ✖ ✔ ✖ ✔ Other courses ✔ ✔ ✔ ✔ University of Sussex Requiring Math ✖ ✔ ✖ ✔ Other courses ✔ ✔ ✔ ✔ King’s College London Requiring Math HL ✖ ✔ ✖ ✔ Other courses ✔ ✔ ✔ ✔ University Of British Columbia Engineering, Commerce, Economics ✖ ✖ ✔ ✔ Other courses ✔ ✔ ✔ ✔ Useful Blog - Top USA Scholarships for Indian IB Diploma Holders & Graduates Useful Blog - IB Scores Required for Ivy League Universities Download FREE IB Study Material Courses and Ebooks available for IB Students (MYP & DP HL SL) from Countries UAE, Singapore, Oman, Qatar, Bahrain, Kuwait, Saudi Arabia, Thailand, Malaysia etcc. In this article, I am going to discuss every topic covered in the IB Maths Standard level and IB Maths higher level along with the number of hours dedicated to each topic. You can download the Complete IB Math Syllabus & IB Maths Book from here. Download Complete IB Maths Syllabus The topics are listed below: Topic 1: Algebra Longer Notes Packet: Series, Complex Numbers, Differentiation FP Packet: Complex Numbers, Theorem of Algebra, Modulus, Exponential Form, Nth Roots of Unit Packet: De Moivre's Theorem, Expansions for Trig Functions, Derivative of sin x Quick Overview Algebraic Sequences Sequences Arithmetic Sequences and Series Geometric Sequences and Series Complex Numbers Arithmetics with Complex Numbers Addition / Subtraction Multiplication Division Argand Diagrams Modulus of a Complex Number Polar Form Multiplication / Division in Polar Form De Moivre's Theorem Applications of the Theorem Roots of Equations Complex Roots Long Division References Topic 2: Functions and Equations Longer Notes Packet: Indices, Surds, Linear, Quadratics, Cubics, Inequalities Packet: Functions, Graphs, Polynomials Quick Overview Concept of Functions Functional Limits Domain Range Number Sets Integers Real Numbers Natural Numbers Combined Functions Graphs of Functions Inverse Function Modulus Functions Logarithms and Exponents Natural Logs Natural Exponent Polynomial Functions Quadratic Formulas and Graphs Graph Transformations Translation Horizontal Vertical Stretch Horizontal Vertical Reflection Horizontal Vertical Modulus Transformations Inverse Transformations Four Things Graph Sketching -Intercepts -Asymptotes -Millionaire Theory -Table -Calculator Topic 3: Circular Functions and Trigonometry Longer Notes Packet: Trigonometry Packet: De Moivre's Theorem, Expansions for Trig Functions, Derivative of sin x Quick Overview Radians Length of Arc Area of a Sector Definitions of Trigonometric Ratios Special Angles Definition of Reciprocal Trigonometric Ratios -Secant -Cosecant -Cotangent Pythagorean Identities Compound Angle Identities Double Angle Identities Manipulation of Trigonometric Functions Inverse Trigonometric Functions -Arcsin -Arccos -Arctan Solving Trigonometric Equations Cosine Rule Sine Rule Area of a Triangle Topic 4: Vectors Longer Notes Packet: Matrices, Vectors Quick Overview Concept of a Vector Representation of Vectors Using Directed Line Segments Unit Vectors and Base Vectors Algebraic and Geometric Vector Calculations Sum and Difference of Two Vectors Special Vectors Scalar Multiplication Magnitude of a Vector Position Vectors Scalar Product of Two Vectors Properties of the Scalar Product The angle between two vectors Perpendicular and Parallel Vectors Vector Equation of a Line The Angle Between Two Lines Distinguishing Between Geometric Cases of Lines Using Vectors Coincident Lines Parallel Lines Intersecting Lines Skew Lines Points of Intersection Vector Product of Two Vectors Properties of the Vector Product Vector Equation of a Plane Vector Equation Normal Form Cartesian Equation of a Plane Intersections With Planes A Line With a Plane Two Planes Angle of Intersections with Planes Line and Plane Plane and Plane Topic 5: Statistics and Probability Longer Notes Packet: Statistics Definitions, Charts and Graphs, Representing data, Standard Deviation Packet: Sets and Probability, Permutations and Combinations, Distributions Quick Overview Measures of Central Tendency (Year 5 Maths) Mean Median Mode Measures of Spread Range Interquartile Range Variance Standard Deviation Adding and Subtracting Mean/Variance Discrete Distributions Uniform / Stick Binomial Geometric Poisson Negative Binomial Continuous Distributions Normal Z-value Probability Density Functions Central Limit Theorem Confidence Limits Hypothesis Testing - Known Variance Type I and Type II Errors Unknown Variance Confidence Limits - Unknown Variance Hypothesis Testing - Unknown Variance Matched Pairs Bivariate Data Probability Generating Functions (PGF) Topic 6: Calculus Longer Notes Packet: Differentiation, Max/Min, Parametrics, Kinematics Packet: Integration, Differentials, Even/Odd Functions, Induction Packet: Harder Integration Questions Quick Overview Differentiation Differentiation by First Principle Exploring the Gradient Function Equations of Tangents and Normals Maximums and Minimums Points of Inflection Rates of Change Kinematics Parametric Equations Integration Exploring the Integral Function Integration Basics Finding Areas from Integrals Volumes of Revolution Separable Differential Equations The Trapezium Rule Options - HL Only- 48 hours IB Math HL students have to study one of the following from the four options: Topic 7: Statistics and Probability Topic 8: Sets, Relations, and Groups Topic 9: Calculus Topic 10: Discrete Mathematics Useful Links IB Mathematics Analysis and Approaches HL Preparation Guide NEW IB MATHEMATICS SYLLABUS 2021
Courses previously available in mathematics (last exam in November 2020):
From August 2019 the following courses were introduced (First assessment in May 2021):
Mathematics: Analysis and Approaches SL
Similar to?
Which Students should take this course?
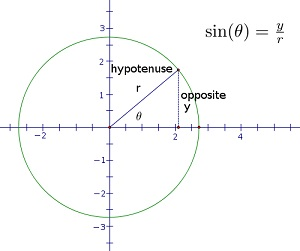
Topics Covered in Math AA SL
Changes Occured From Previous SL




![]()

Mathematics: Analysis and Approaches HL
Similar to?
Which Students should take this course?
Topics Covered in Math AA HL
Changes Occured From Previous HL




![]()

Mathematics: Applications and Interpretation SL
Similar to?
Which Students should take this course?
Topics Covered in Math AI SL
Changes Occured From Previous SL




![]()

Mathematics: Applications and Interpretation HL
Similar to?
Which Students should take this course?
Topics Covered in Math AI HL
Changes Occured From Previous HL




![]()

University Acceptance of IB Math
The Complete IB Maths Syllabus: SL & HL
If you are going through this syllabus, I suppose you are interested in taking this course or you are presently joined with this course.
IB (International Baccalaureate) Math HL Online Preparation:
For IB Maths AA/AI SL, dedicated hours are 140 hours and for IB Maths AA/AI HL, dedicated hours are 182 hours
Are you Looking For FREE IB Past Year Papers, Notes, and FREE Ebooks Like Oxford, Cambridge, IBDP Publications. Just Click on the below Image. Fill the Form and Download all the PDF Files.